Generating Jordan, 5

There is a Jordan curve such that every piecewise-linear path from the inside to the outside intersects the curve infinitely many times. I define the wiggling precisely here in terms of courses (turn-type sequences).

Local wiggling to triples

Last time I described the local picture of a wiggled hex curve. That is, given a hex curve $\gamma$ and a triangle $T$ with a turn of $\gamma,$ I described what $f(\gamma) \cap T$ looks like, and gave a picture of this. Our task now is to draw a hex curve wiggled several times.

Our preferred representation of a hex curve is its course, i.e. its sequence of turn-types. The local picture in a triangle always wiggles to three oriented components, yielding three courses. We want to specify triples of courses of the sort one gets by taking the courses of such unions of oriented components in a sequence of consecutively adjacent triangles.

More specifically, let us say an (intermediate) triple is a triple of courses $trp = (\mu, \upsilon, \kappa)$ such that for some triangles $t_0$ and $t_\nu$ (possibly the same), + $\mu$ beginning at $t_{0,3}^A$ ends at $t_{0,4}^A;$ + $\upsilon$ beginning at $t_{0,5}^A$ ends at $t_{\nu,3}^F;$ and + $\kappa$ beginning at $t_{\nu,4}^F$ ends at $t_{\nu,5}^F.$ Fixing $t_0$ and a bend in $t_0$ determines $t_\nu.$

In the previous post we worked out what these triples were for $f(\gamma) \cap t$ when $t$ contained a port turn. As in that post, we label the components of $f(\gamma) \cap t$ variously $M_t,$ $Y_t,$ and $C_t.$ Recall that

• $M$ starts from $t_3^A$ with course $PSPSSSSPSPS,$ and thus ends at $t_4^A;$
• $Y$ starts from $t_5^A$ with course $PSPSPSPPSPS,$ and thus ends at $t_3^F;$ and finally,
• $C$ starts from $t_4^F$ with course $PSPSSPSPSPSPPPPSPSPSPSPPSPS,$ and thus ends at $t_5^F.$

We express this in Python as follows:

P_becomes = ("PSPSSSSPSPS","PSPSPSPPSPS","PSPSSPSPSPSPPPPSPSPSPSPPSPS")

Suppose we follow that port turn in a triangle $t$ with a starboard turn in another triangle $t'.$ For the starboard turn in $t',$ we get the following, mutatis mutandis:

• $M$ starts from ${t'}_3^A$ with course $PSPSSPSPSPSPSSSSPSPSPSPPSPS,$ and thus ends at ${t'}_4^A;$
• $Y$ starts from ${t'}_5^A$ with course $PSPSSPSPSPS,$ and thus ends at ${t'}_3^F;$ and finally,
• $C$ starts from ${t'}_4^F$ with course $PSPSPPPPSPS,$ and thus ends at ${t'}_5^F.$

(The ordering of triangles along the given sides of $t'$ are also from port to starboard.) We can express this likewise in Python as follows:

S_becomes = ("PSPSSPSPSPSPSSSSPSPSPSPPSPS","PSPSSPSPSPS","PSPSPPPPSPS")

(The reader may check that if $P_b$ is the former triple shown and $S_b$ the latter, then these triples are related by $flip(P_b) = S_b,$ where the function $flip$ reverses each string in the triple, swaps $P$ with $S$ and vice versa, and reverses the triple, as in the following code.)

def flip(trp):
    lst = list(trp)
    lst = [list(reversed(path)) for path in lst]
    swap = lambda tok: "P" if tok == "S" else "S"
    lst = [[swap(tok) for tok in path] for path in lst]
    return tuple(reversed(lst))

Thus the following statements hold: + $M_t$ intersects no components of $f(\gamma) \cap t';$ + $C_{t'}$ intersects no components of $f(\gamma) \cap t;$ + $Y_t$ ends at $t_3^F;$ + $M_{t'}$ begins at ${t'}_3^A$ and ends at ${t'}_4^A;$ + $C_t$ begins at $t_4^F$ and ends at $t_5^F;$ and finally, + $Y_{t'}$ begins at ${t'}_5^A.$

Joining triples

The union of all these components in the union $t \cup t'$ therefore again has three oriented components. Two components have not been fitted together with others. The first is the $M$ component of $f(\gamma) \cap t.$ The latter is the $C$ component of $f(\gamma) \cap t'.$ Finally, the middle component is composed of the four other components. Considering the components as oriented arcs, and labelling them $M,Y,C$ in $t$ and $M',Y',C'$ in $t'$ in that order, we have that $f(\gamma) \cap (t \cup t')$ is also the union of three oriented components, to wit $M, Y\ast M' \ast C \ast Y', C'$ in that order.

The same incidence relations hold, with different courses, when following port with port, starboard with port, or starboard with starboard. Port to starboard and starboard to starboard are depicted in the following figure.

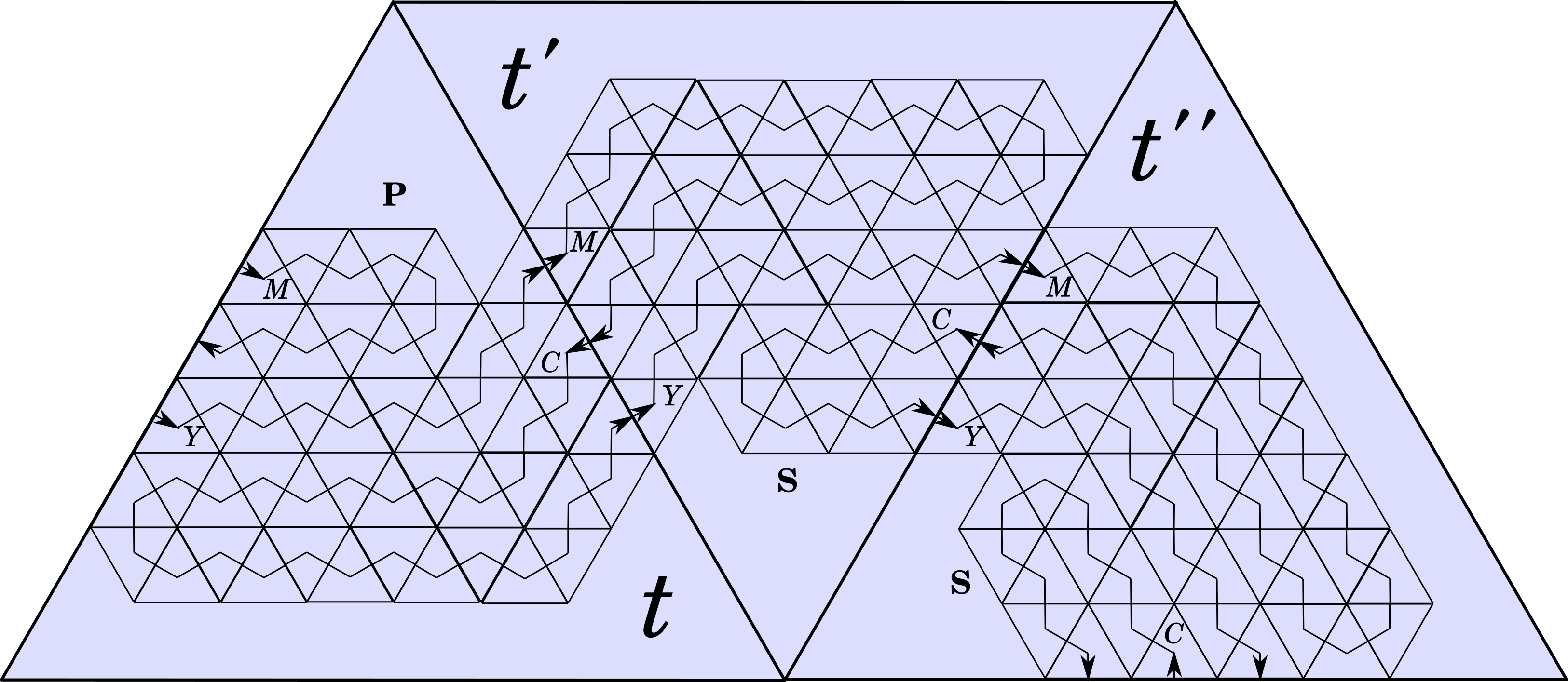
Thus, if $trp = (M, Y, C)$ and $trp' = (M', Y', C')$ are two intermediate triples, we define their join $trp \ast trp'$ to be $(M, Y\ast M' \ast C \ast Y', C').$

def join(trp0, trp1):
    (m, y, c) = trp0
    (mp,yp,cp) = trp1
    return (m, y+mp+c+yp, cp)

Wiggling a course

Let $Tok = \{P,S\}.$ Let $Tok^\ast$ be the set of courses. Following the above, we define the function $wgl: Tok \to Tok^\ast \times Tok^\ast \times Tok^\ast$ as follows:

$$\begin{multline} wgl(P) = (PSPSSSSPSPS, PSPSPSPPSPS, \\ PSPSSPSPSPSPPPPSPSPSPSPPSPS), \end{multline}$$

$$\begin{multline} wgl(S) = (PSPSSPSPSPSPSSSSPSPSPSPPSPS, \\ PSPSSPSPSPS, PSPSPPPPSPS), \end{multline}$$

so that $wgl(S) = flip(wgl(P)).$ Then, given a course $\Gamma = k_0 k_1 \cdots k_{n-1}$ (with $k_i \in Tok$), we define $wiggle(\Gamma) = wgl(k_0) \ast wgl(k_1) \ast \cdots \ast wgl(k_{n-1}).$ (This is well-defined since $wgl$ is associative.)

With this definition we have almost determined the course of $f(\gamma)$ given the course $\Gamma$ of $\gamma.$ The above gives us that $f(\gamma)$ is the union of three hex curves whose three courses are those in the triple $wiggle(\Gamma).$ It remains to determine how to join these courses. Now, $wiggle(\Gamma)$ is a triple $(MM, YY, CC)$ beginning in some triangle $t$ and ending in some triangle $T.$ Assuming $\Gamma$ is the course of a closed hex curve, likewise $wiggle(\Gamma)$ is too. Thus the aft side of $t$ and the fore side of $T$ coincide. So $t_i^A$ and $T_i^F$ coincide along these sides for $i \in \{3,4,5\}.$ Now, $YY$ ends at $T_3^F$ and $MM$ begins at $t_3^A;$ $MM$ ends at $t_4^A$ and $CC$ begins at $T_4^F;$ and finally $CC$ ends at $T_5^F$ and $YY$ begins at $t_5^A.$ Thus the complete course of $f(\gamma)$ is $YY\ast MM\ast CC.$

def wiggle(tokens):
    trps = map(lambda tok: P_becomes if tok == 'P' else S_becomes, tokens)
    tot = trps.__next__()
    for trp in trps:
        tot = join(tot,trp)
    (MM,YY,CC) = tot
    return YY + MM + CC