Thick and thin

Mostly math with Robert

Generating Jordan, 4

There is a Jordan curve such that every piecewise-linear path from the inside to the outside intersects the curve infinitely many times. I sketch the construction of such a curve here.

Triangles instead

Last time I described the very simple class of rectagons. I also gave a way to represent these curves different as a sequence of movement tokens. There were three movement tokens: left, right, and straight. For simplicity’s sake, it would be most convenient only to have two movement tokens. (Such curves would be arguably more “digital” than the previous curves.) I was unable to get this to work for a grid of squares. Parity problems got in the way. So I ditched the squares and used equilateral triangles instead.

For triangles, there is no straight movement token. Only Port and Starboard movements are possible. The question is what the local picture of a wiggling of the curve should be. Happily the picture will look the same in all triangles.

Note that we don’t want an isotopy of the curve fixing the boundary of the triangle. No such triangle-local isotopy can give us the sort of Jordan curve we want. The triangle edges would end up being piecewise-linear paths from the inside to the outside. Instead we just show the intersection of the triangle with the wiggled curve.

Hex curves and turns

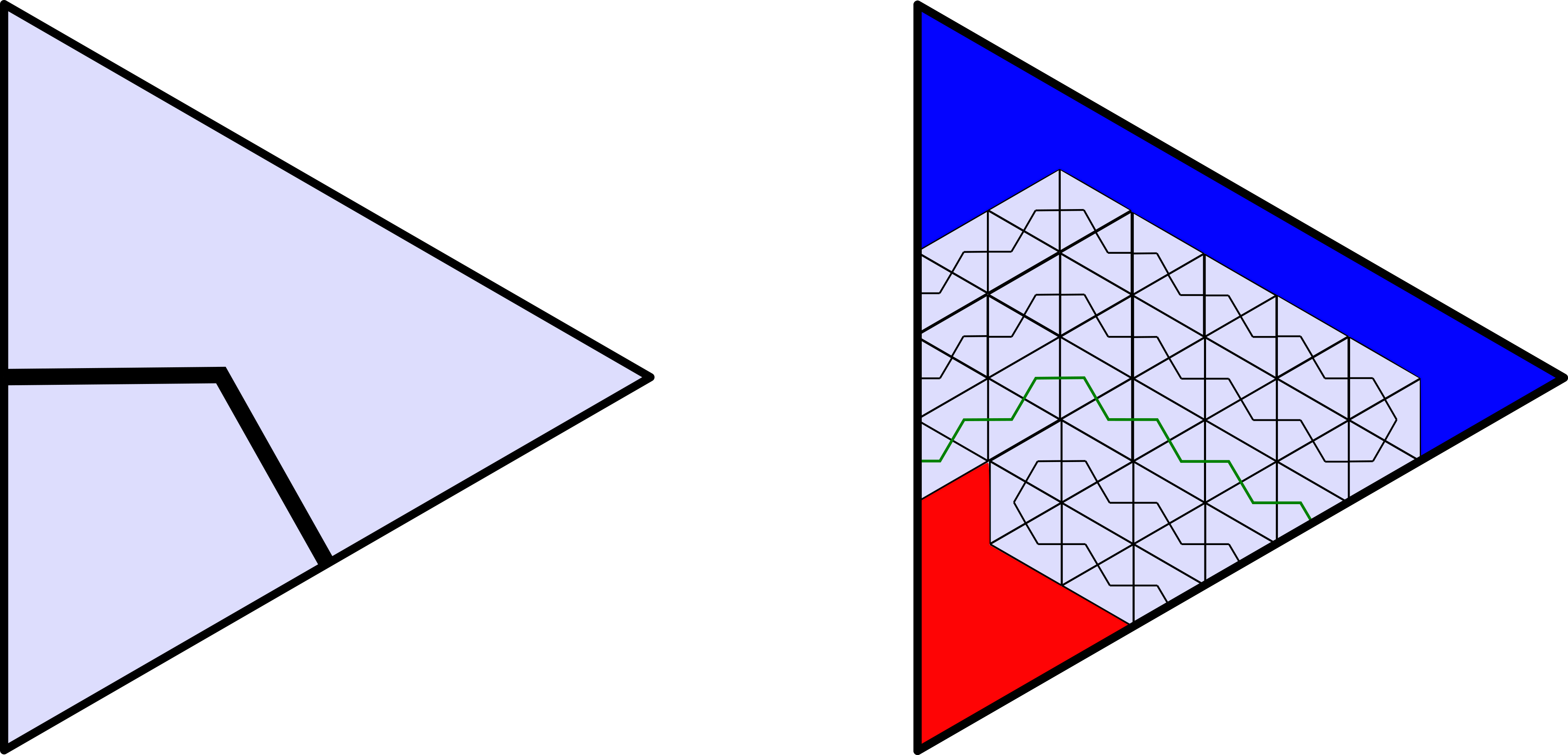
More formally, suppose TT is an equilateral triangle. Let CC be its centroid. A bend in TT is the union of two feet from CC perpendicular to two sides of T.T. There are three bends in every triangle. Suppose PPPP is a 6-regular triangulation of the plane by equilateral triangles. A hex curve subordinate to PPPP is a PL curve that is the union of bends in triangles of PP.PP.

An oriented bend is a turn. Every triangle has six turns possible in it. The turns have two orbits under the three rotational symmetries of T.T. One orbit consists of port turns; the other consists of starboard turns. Up to orientation-preserving isometry, a oriented hex curve is determined by its corresponding sequence of port and starboard symbols “P” and “S,” which we will call its course.

Our aim is to give a function ff from hex curves to hex curves, such that * f(γ)f(\gamma) is isotopic to γ;\gamma; * for all hex loops γ,\gamma, γ∞=lim⁡n→∞f∘n(γ)\gamma_\infty = \lim_{n\to \infty} f^{\circ n}(\gamma) is a Jordan curve; and * for all hex loops γ,\gamma, every piecewise-linear path between the inside and outside of γ∞\gamma_\infty intersects γ∞\gamma_\infty in infinitely many points.

The turn-local picture of a wiggling

As with wiggling the rectagons, a wiggled hex curve will no longer be subordinate to its original triangulation. Instead, the new curve is subordinate to a finer triangulation. For our choice of f,f, the new triangulation has eighty-one triangles per previous triangle, dividing the sides of the triangles into nine equal pieces. Equivalently, the new triangulation is the old triangulation scaled down by a factor of nine by homothety at a vertex.

The local picture γ′∩T\gamma' \cap T of the wiggling is the same for both orientations of a bend. However, it is most convenient to give the local picture via its courses. This requires orientations. So I will give the courses (and starting triangles) for the components of the local picture after wiggling a port turn, and after wiggling a starboard turn.

Suppose we want to wiggle a port turn. Let AA be the side at which the turn begins, and FF the side at which it ends. Then the other side SS of the triangle is starboard of the (port) turn, and the vertex is port of the turn. Nine new triangles are incident to A.A. Order them T0A,…,T8AT_0^A,\ldots,T_8^A from port to starboard. Likewise, nine new triangles are incident to F.F. Order them T0F+,…,T8FT_0^F+,\ldots,T_8^F from port to starboard. The components’ boundary points lie in the triangles T3A,F,T4A,F,T5A,F.T_3^{A,F},T_4^{A,F},T_5^{A,F}. To wit, the (three) components of f(γ)∩Tf(\gamma) \cap T are as follows:

  • MM starts from T3AT_3^A with course PSPSSSSPSPS,PSPSSSSPSPS, and thus ends at T4A;T_4^A;
  • YY starts from T5AT_5^A with course PSPSPSPPSPS,PSPSPSPPSPS, and thus ends at T3F;T_3^F; and finally,
  • CC starts from T4FT_4^F with course PSPSSPSPSPSPPPPSPSPSPSPPSPS,PSPSSPSPSPSPPPPSPSPSPSPPSPS, and thus ends at T5F.T_5^F.

Here is what that looks like in the triangle of a bend:

Wiggling the local picture in a triangle.

Curiously the courses all start and end with the sequence PSPS.PSPS.